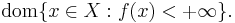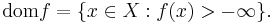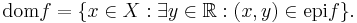Effective domain

In convex analysis, a branch of mathematics, the effective domain is an extension of the domain of a function.

Given a vector space X then a convex function mapping to the extended reals, 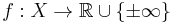$f: X \to \mathbb{R} \cup \{\pm \infty\}$ , has an effective domain defined by

$\operatorname{dom}\{x \in X: f(x) < %2B\infty\}. \,$ ^[1]^[2]

If the function is concave, then the effective domain is

$\operatorname{dom}f = \{x \in X: f(x) > -\infty\}. \,$ ^[1]

The effective domain is equivalent to the projection of the epigraph of a function 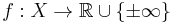$f: X \to \mathbb{R} \cup \{\pm \infty\}$ onto X. That is

$\operatorname{dom}f = \{x \in X: \exists y \in \mathbb{R}: (x,y) \in \operatorname{epi}f\}. \,$ ^[3]

Note that if a convex function is mapping to the normal real number line given by 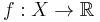$f: X \to \mathbb{R}$ then the effective domain is the same as the normal definition of the domain.

A function 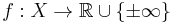$f: X \to \mathbb{R} \cup \{\pm \infty\}$ is a proper convex function if and only if the effective domain of f is nonempty and 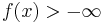$f(x) > -\infty$ for every 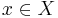$x \in X$ .^[3]

References

^ ^a ^b Aliprantis, C.D.; Border, K.C. (2007). Infinite Dimensional Analysis: A Hitchhiker's Guide (3 ed.). Springer. p. 254. doi:10.1007/3-540-29587-9. ISBN 978-3-540-32696-0.
^ Föllmer, Hans; Schied, Alexander (2004). Stochastic finance: an introduction in discrete time (2 ed.). Walter de Gruyter. p. 400. ISBN 9783110183467.
^ ^a ^b Rockafellar, R. Tyrrell (1997) [1970]. Convex Analysis. Princeton, NJ: Princeton University Press. p. 23. ISBN 9780691015866.